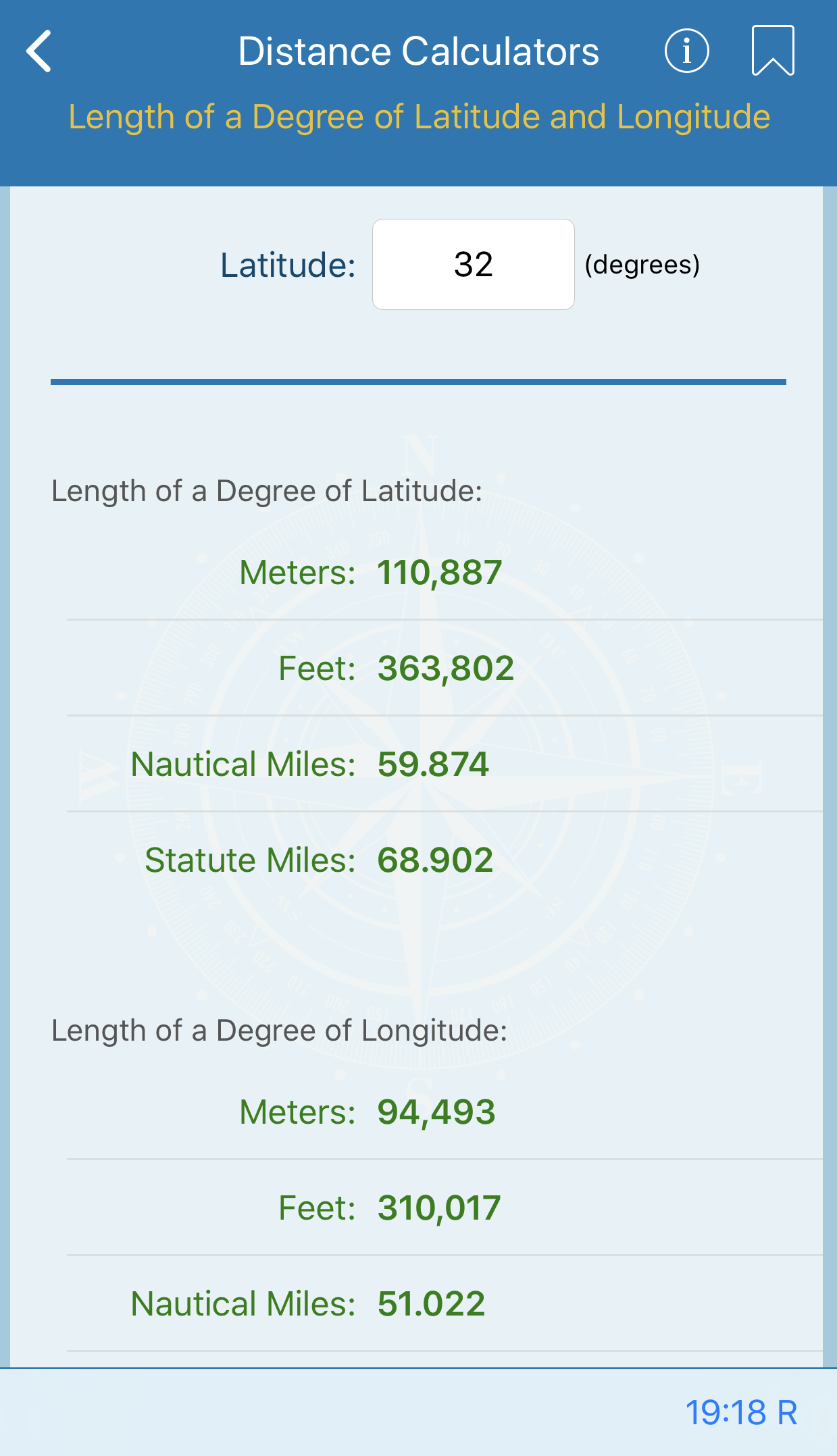
Length of a Degree of Latitude and Longitude
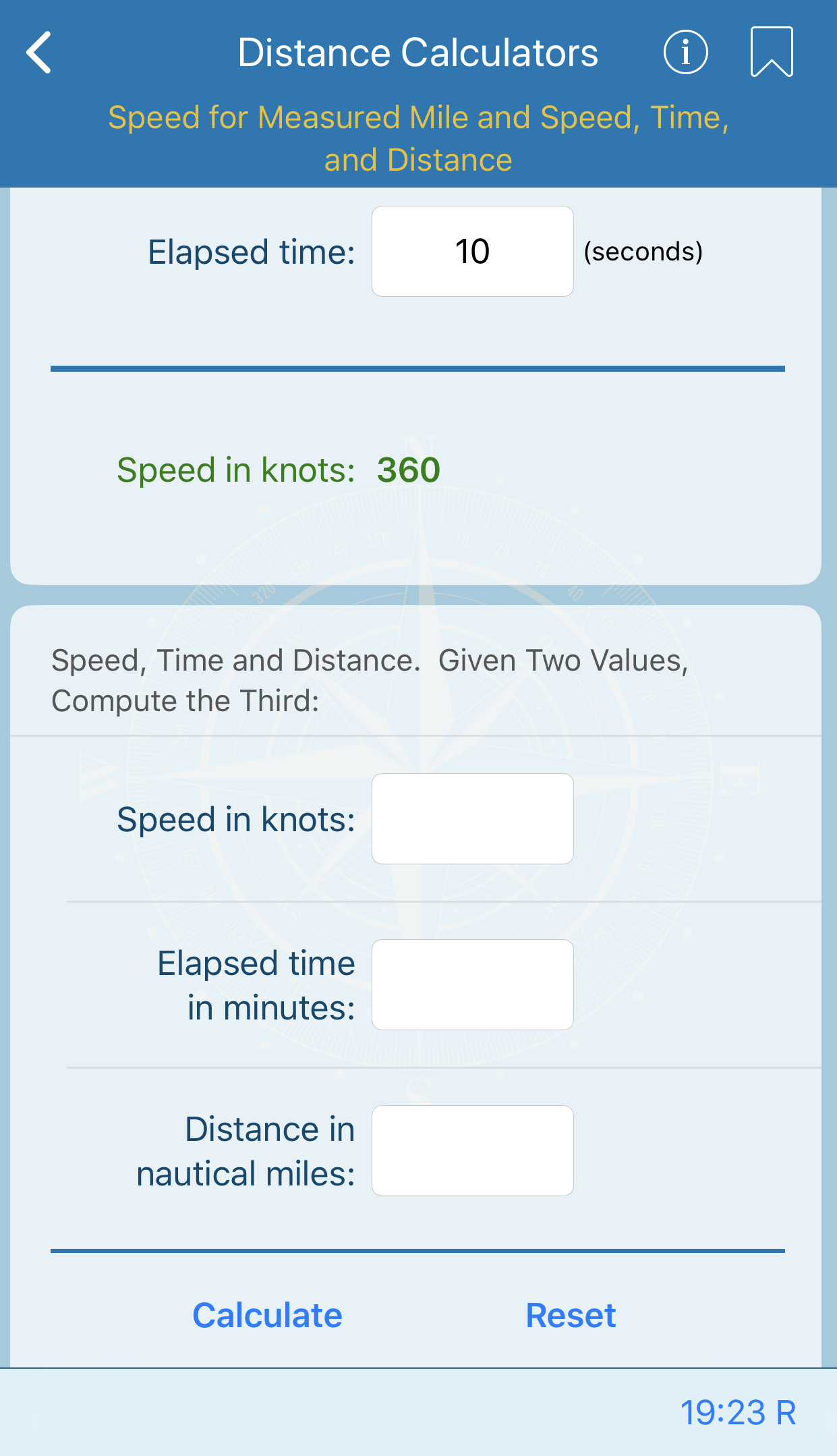
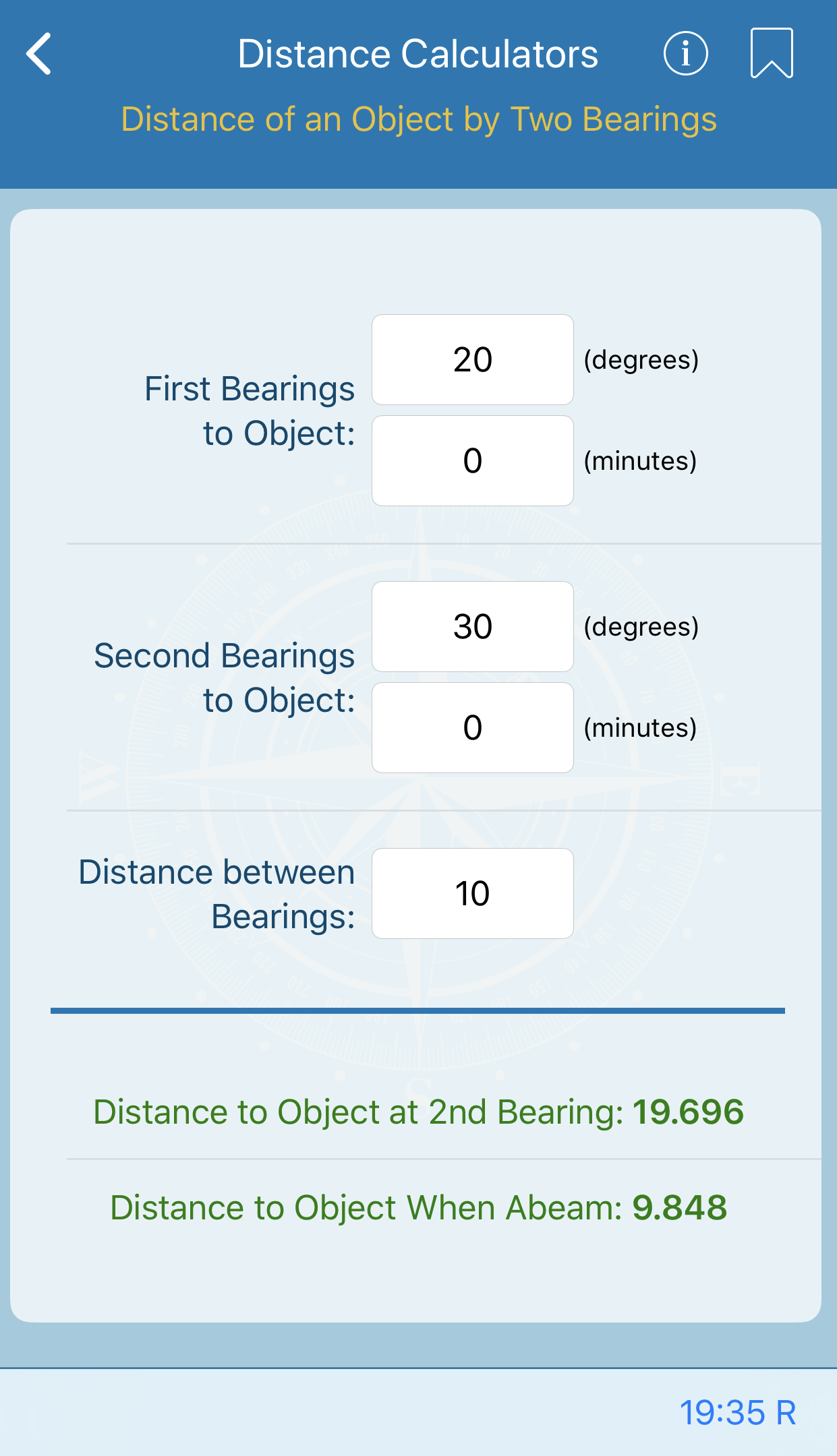
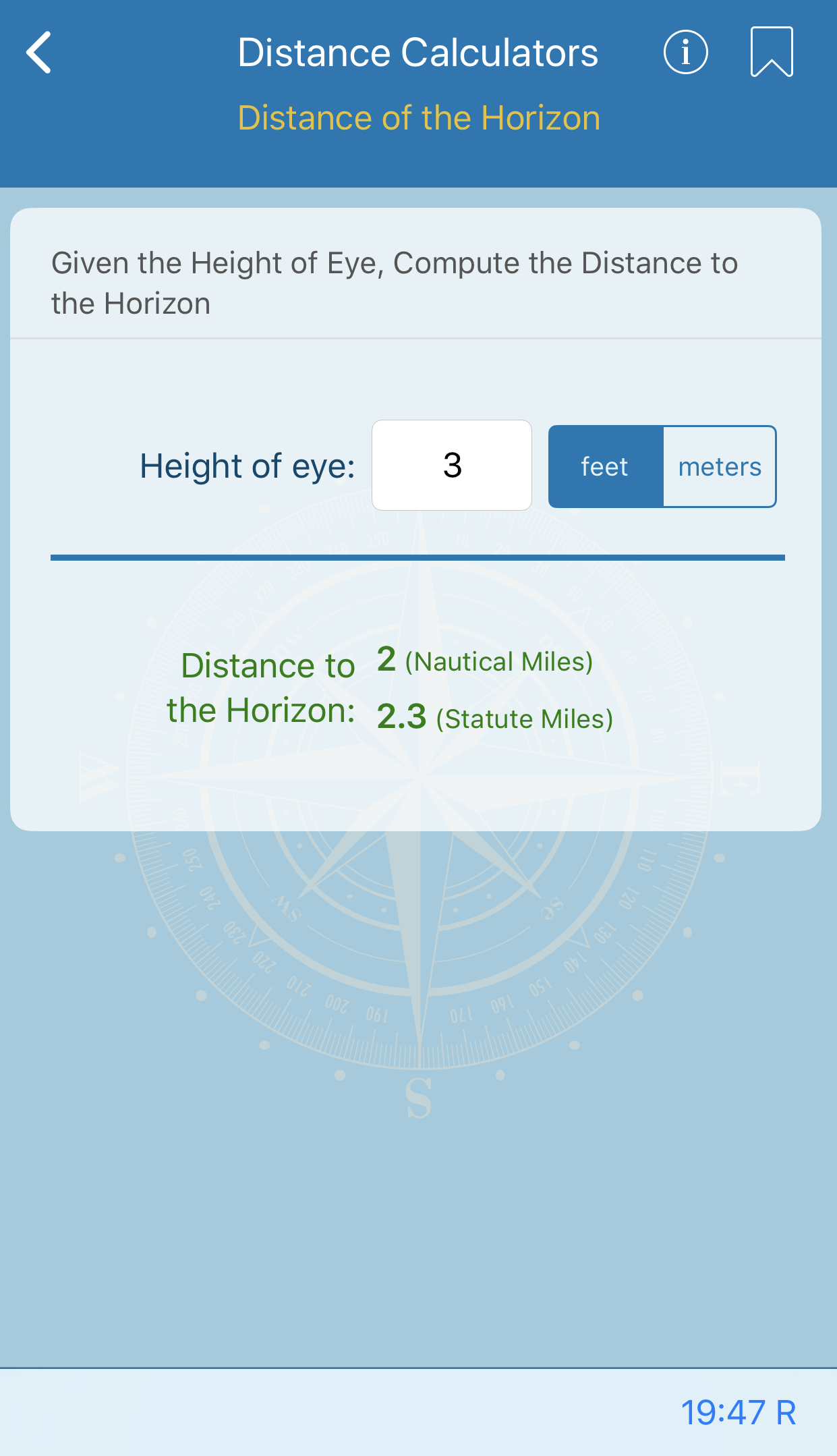
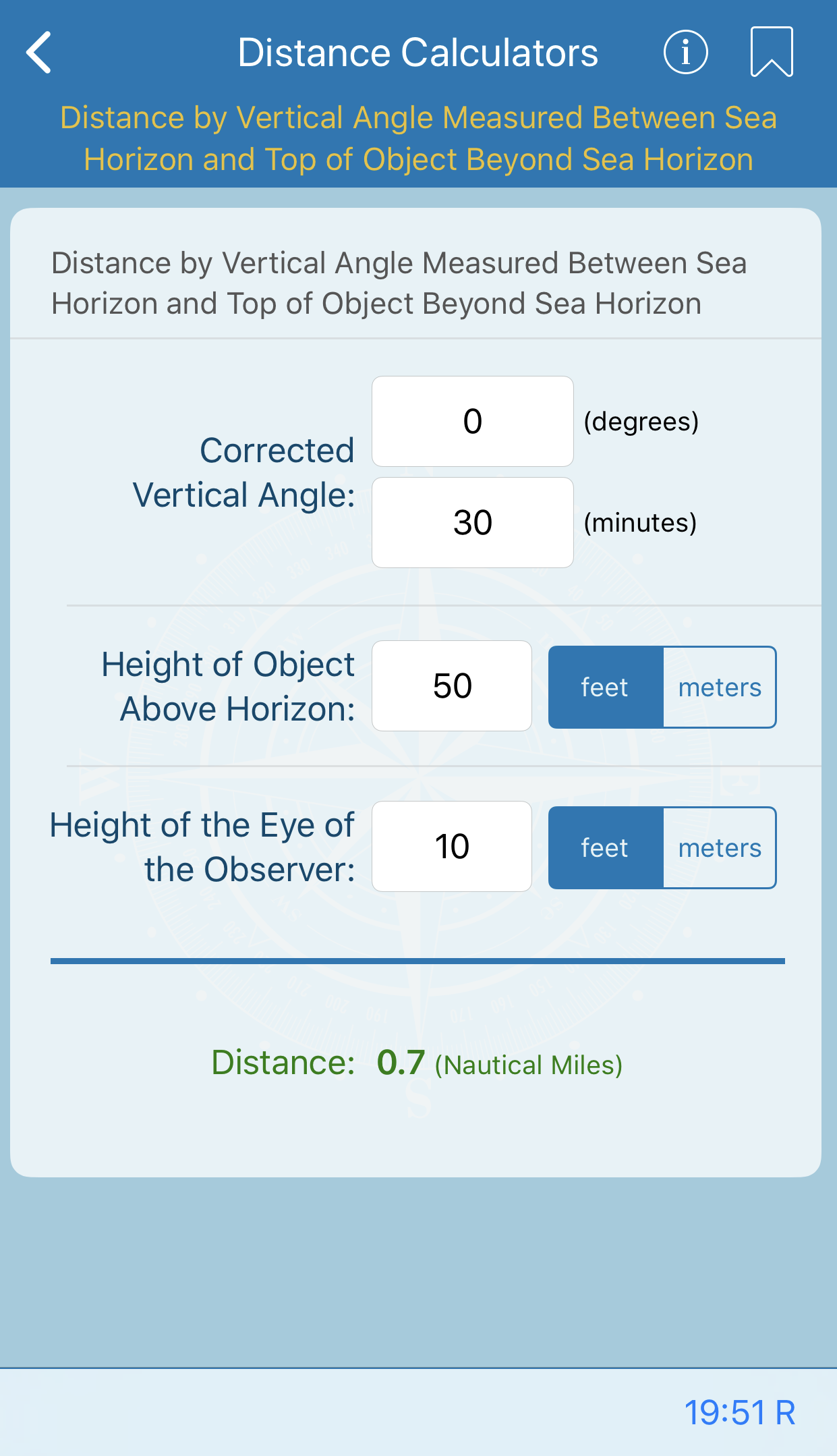
This calculation gives the length of one degree of latitude and longitude at intervals of 1° from the equator to the poles. Lengths are given in nautical miles, statute miles, feet, and meters.
The values were computed in meters, using the World Geodetic System ellipsoid of 1972, and converted to other units.