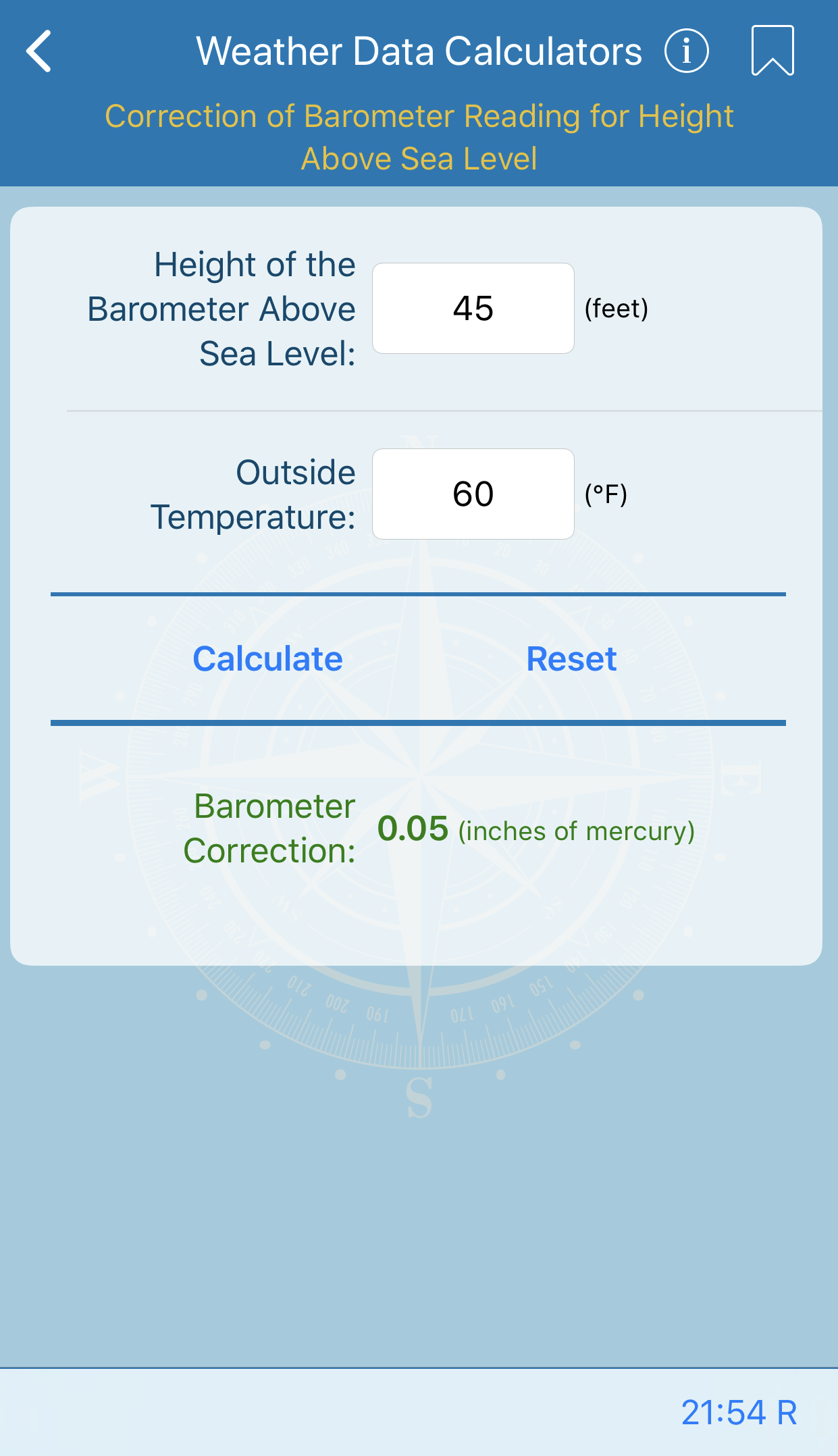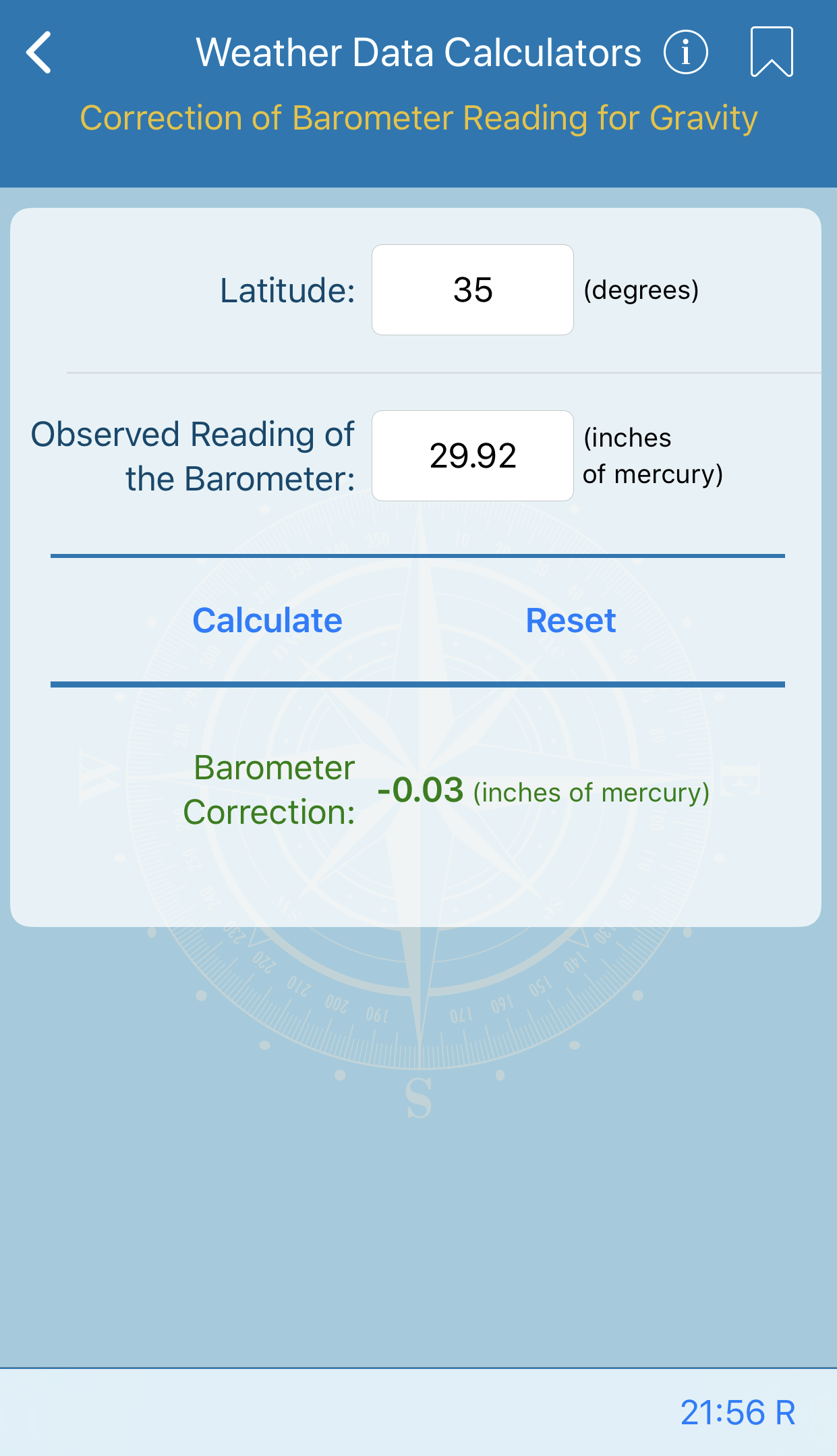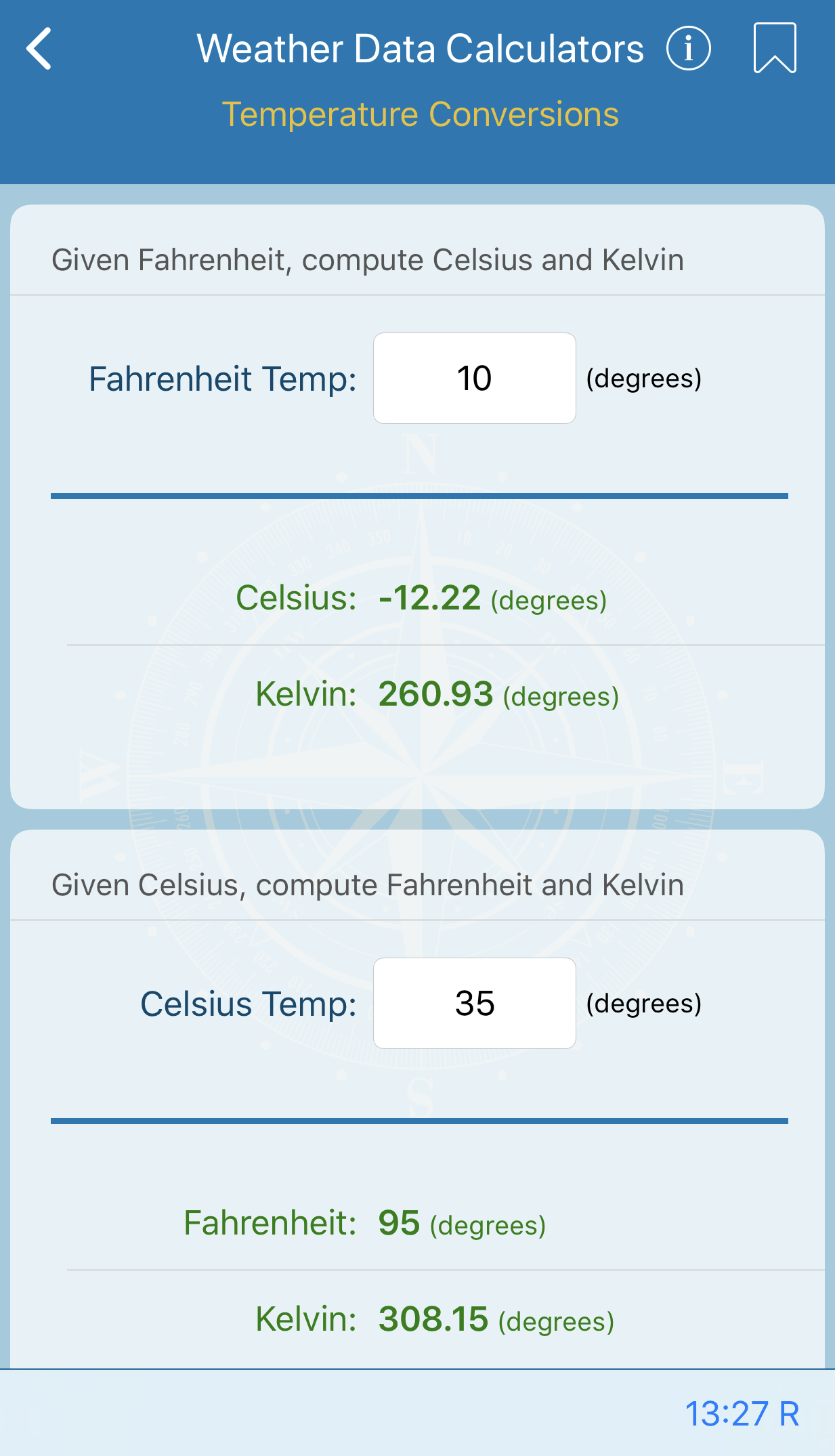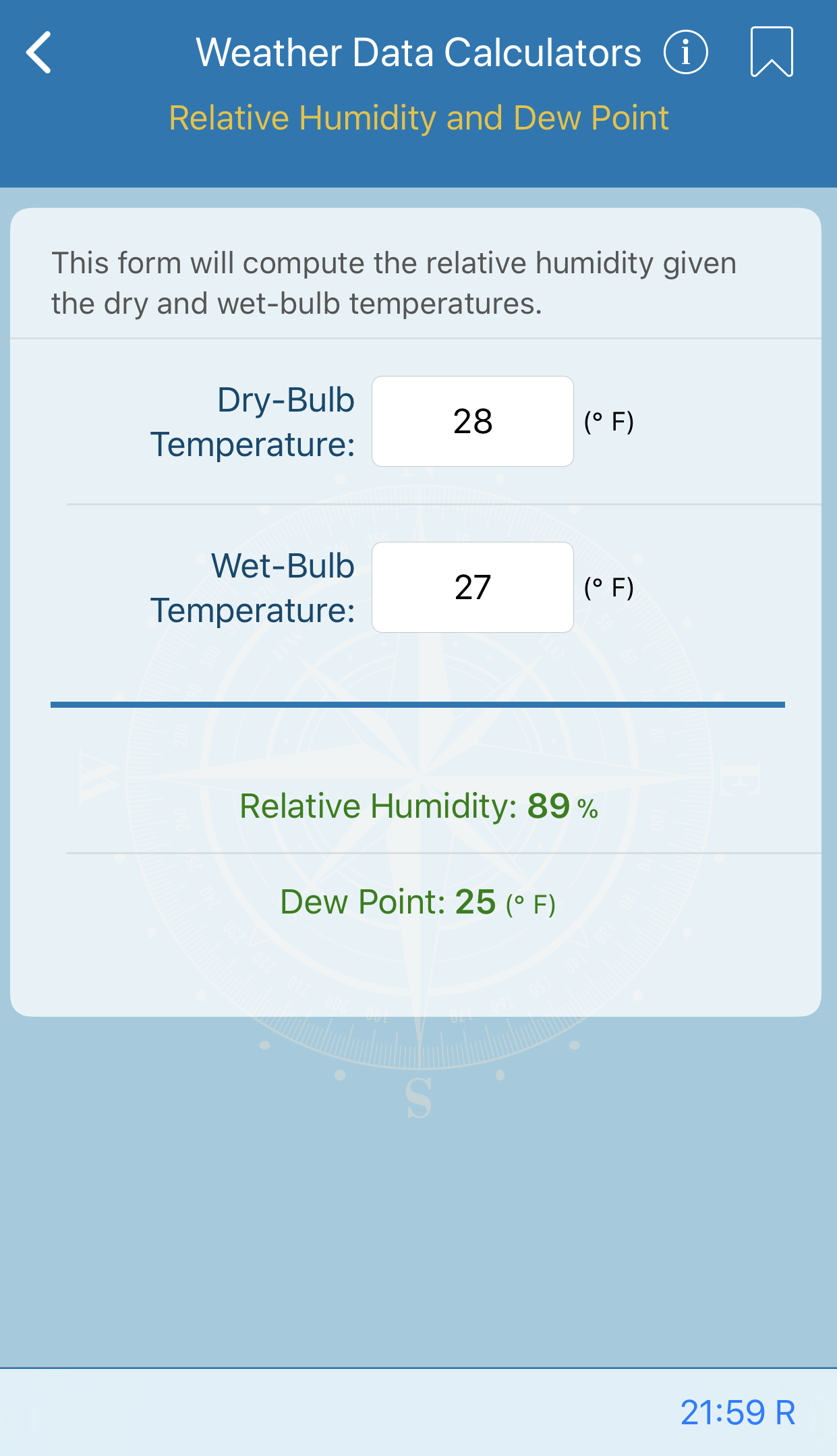
Direction and Speed of True Wind, Corrections for Barometer Readings, Temperature Conversions and more.
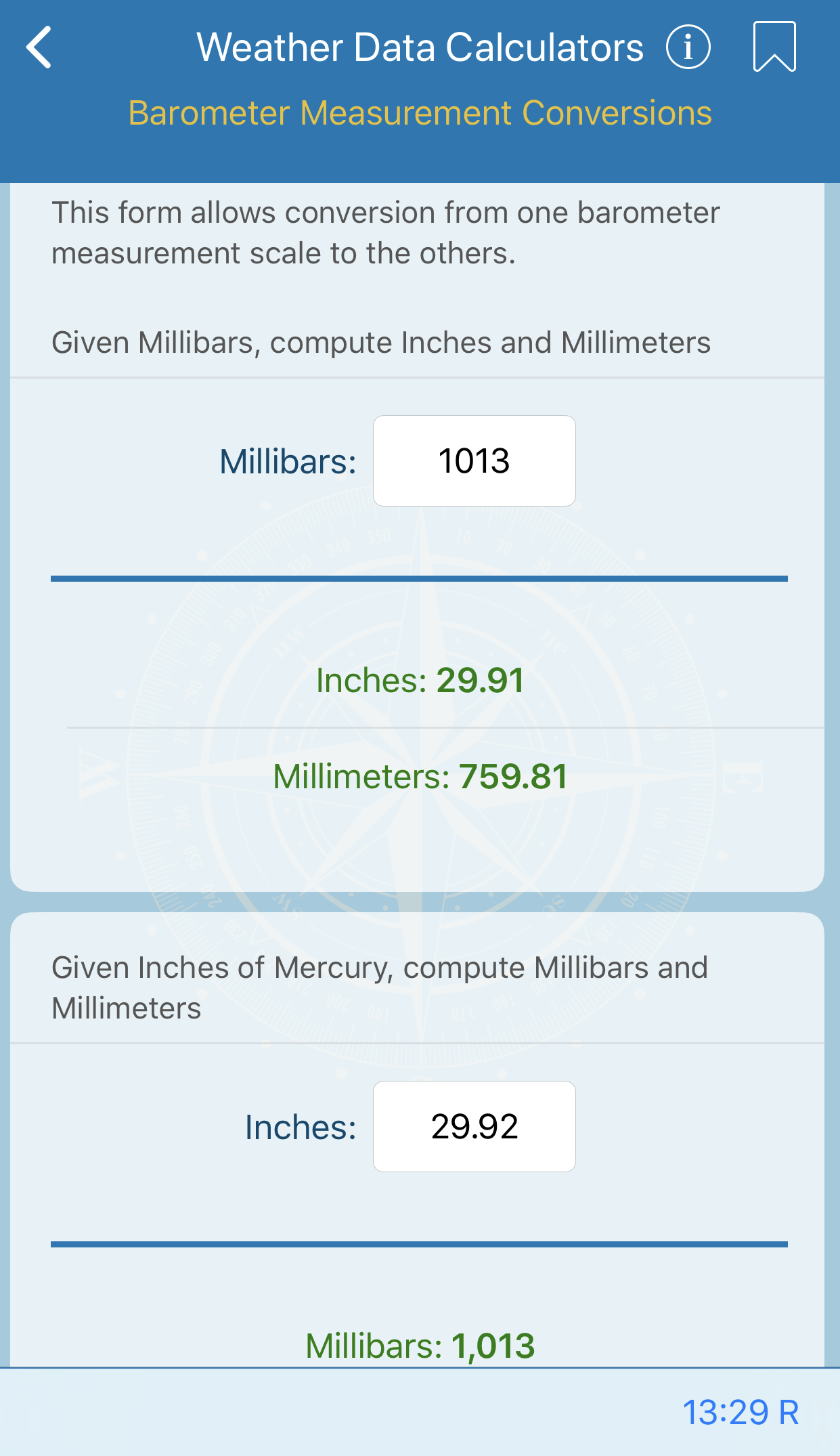
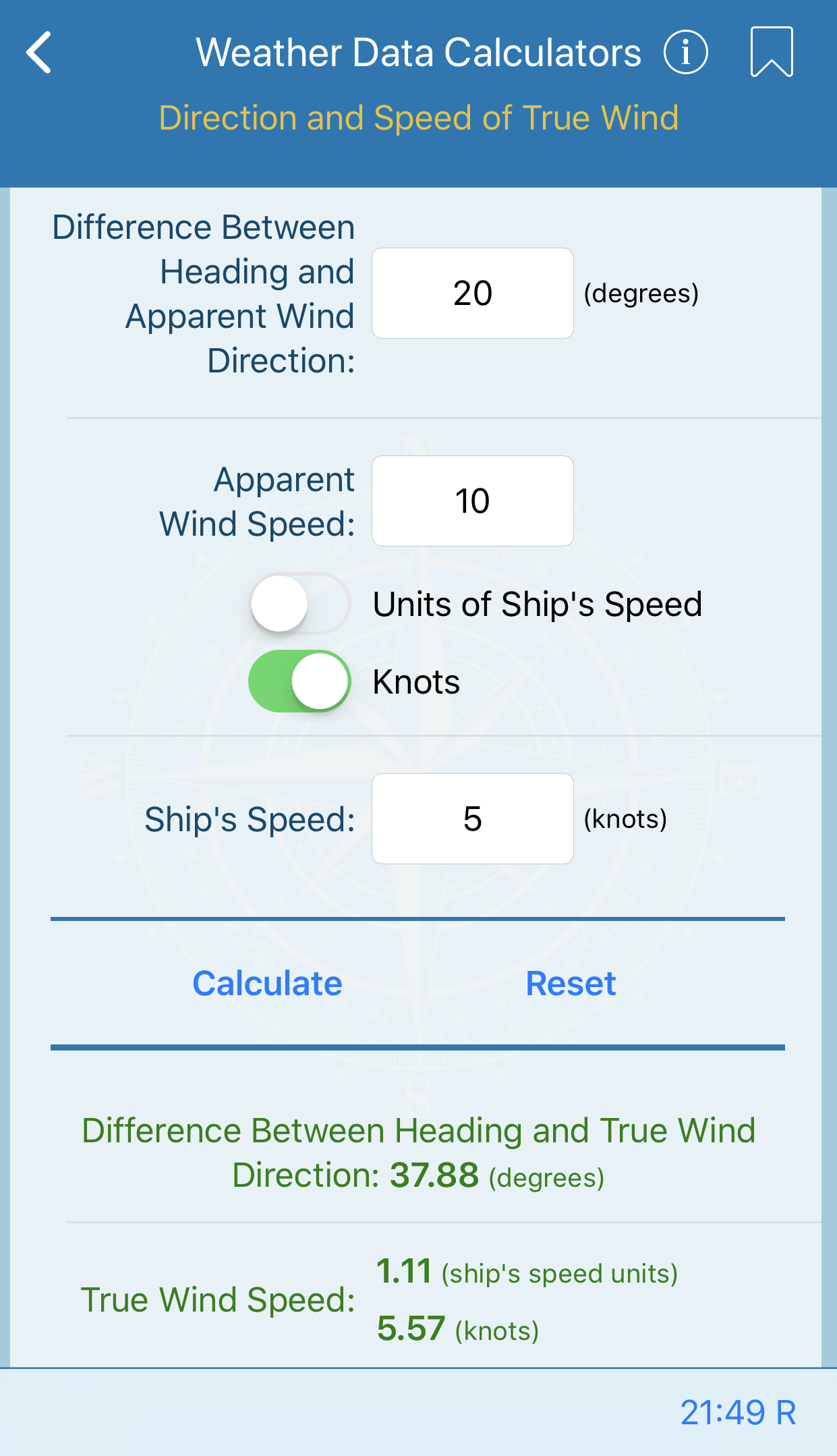
This form will compute the difference between ship heading and true wind direction and true wind speed. Difference between ship heading and apparent wind direction and apparent wind speed must be provided.
Note that if apparent wind speed is supplied in knots, it is necessary to supply the ship speed in knots.
If simultaneous barometer readings at different heights are to be of maximum value in weather analysis, they should be converted to the corresponding readings at a standard height, usually sea level.
To convert the observed barometer reading to this level, enter the outside temperature and the height of the barometer above sea level. The height of a barometer is the height of its sensitive element; in the case of a mercurial barometer, this is the height of the free surface of the mercury in the cistern.
The correction calculated here applies to the readings of any type barometer and is always added to the observed readings unless the barometer is below sea level.
The height of the column of a mercury barometer is affected by the force of gravity, which changes with latitude and is approximately equal along any parallel of latitude. The average gravitational force at latitude 45°32'40" is used as the standard for calibration.
This calculation provides a correction to convert the observed reading at any other latitude to the corresponding value at latitude 45°32'40".
Enter the latitude, and the observed barometer reading, tap 'Calculate,' then apply the correction in accordance with the (+/-) sign given. This correction does not apply to aneroid barometers.
The formula uses these constants:
1. density of mercury = 13.5951 grams per cubic centimeter
2. standard gravity = 980.665 dynes
This calculation converts Fahrenheit, F; Celsius (centigrade), C; or Kelvin, K; temperature scales.
On the Fahrenheit scale, the freezing temperature of pure water at standard sea level pressure is 32°, and the boiling point under the same conditions is 212°. The corresponding temperatures are 0° and 100° on the Celsius scale and 273.15° and 373.15°, respectively, on the Kelvin scale.
The value of (–) 273.15° C for absolute zero, the starting point of the Kelvin scale, is the value recognized officially by the National Institute of Standards and Technology (NIST).
The formulas are:
C = 5/9(F × 32°)= K – 273.15°
F = 9/5C+32°= 9/5 K–459.67°
K = 5/9(F – 459.67°)= C + 273.15°
To determine the relative humidity of the atmosphere, enter the dry-bulb (air) temperature (F), and the difference between the dry-bulb and wet-bulb temperatures (F).
The calculation displays the approximate percentage of relative humidity and dew point in degrees Fahrenheit.
If the dry-bulb and wet-bulb temperatures are the same, relative humidity is 100 percent, and the air is at or below the dew point.
Because of the difference in expansion of the mercury column of a mercurial barometer and that of the brass scale by which the height is measured, a correction should be applied to the reading when the temperature differs from the standard used for calibration of the instrument.
To find the correction, enter the temperature in degrees Fahrenheit and the barometer reading. Apply the correction in accordance with the (=/-) sign given. This correction does not apply to aneroid barometers.
The standard temperature used for calibration is 32° F for the mercury, and 62° F for the brass.
This calculation allows conversion from one barometer measurement scale to another including millibars, millimeters of mercury, and inches of mercury.
The formula uses these constants:
1. density of mercury = 13.5951 grams per cubic centimeter
2. standard gravity = 980.665 dynes
Aviation Mobile Apps, LLC
8501 Astronaut Blvd STE 170
Cape Canaveral, FL 32920
Email: Customer Service
Phone: +1 (800) 207-7142
Phone: +1 (682) 444-1822